Da binario a decimale.
Si rappresenta il numero binario in forma polinominale e si sommano i valori decimali dei singoli termini del polinomio,
1011 = 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 = 8 + 0 +2 + 1 = 1110
11,01 = 1 x 21 + 1 x 20 + 0 x 2-1 + 1 x 2-2 = 2 + 1 + 0 + 0,25 = 3,25
Da decimale a binario.
Nel caso del numero intero si può fare con il “metodo delle successive divisioni per due”. Si effettua la divisione della cifra per 2 il resto della divisione costituisce la cifra meno significativa, si procede cosi sul quoziente fino a quando quest’ultimo non si annulla:
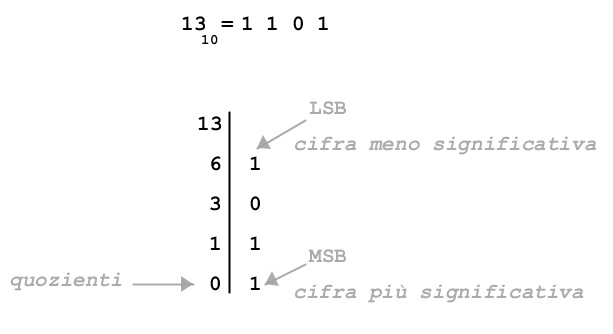
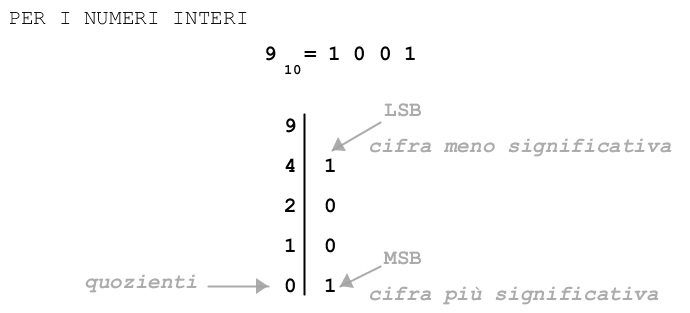
Metodo delle successive moltiplicazioni per due.
Nel caso di numeri frazionari con parte intera nulla, il metodo consiste nel moltiplicare per due il numero decimale a parte intera nulla poiché il numero è minore di 1, moltiplicando per 2 si ottiene un numero compreso tra 0 e 2 (escluso):la parte intera (o e 1) rappresenta il bit più significativo del numero binario. Si procede ora a moltiplicare per 2 la parte frazionaria del numero precedentemente attenuto e si ottiene un numero la cui parte intera rappresenta un altro bit del numero binario, mentre la parte frazionaria viene ancora moltiplicata per 2.
Il metodo prosegue fino all’annullamento della parte frazionaria o fino a quando la precisione della conversione risulta sufficiente.
0,32510=0,01012 ..
- 0,325 x 2 =0,625 0 MSB
- 0,625×2 =1,25 1
- 0,25×2=0,5 0
- 0,2×2=1 1 LSB

